Charles' Law of Volumes

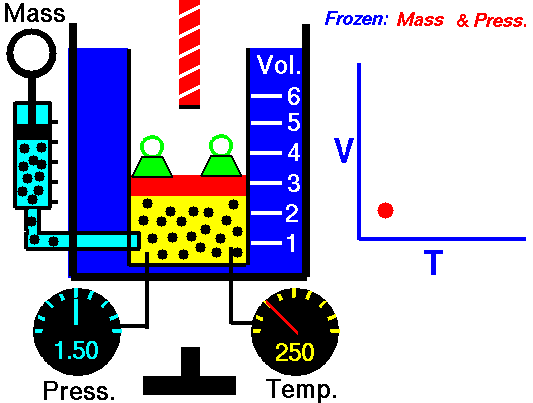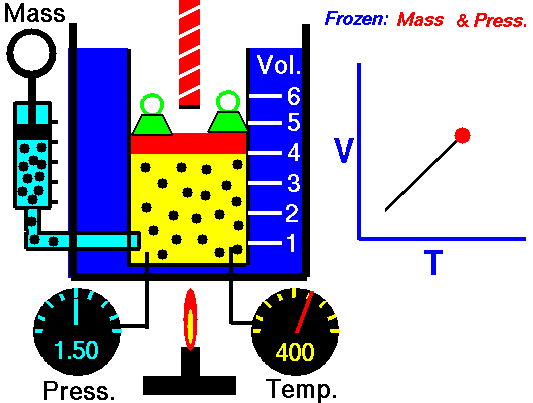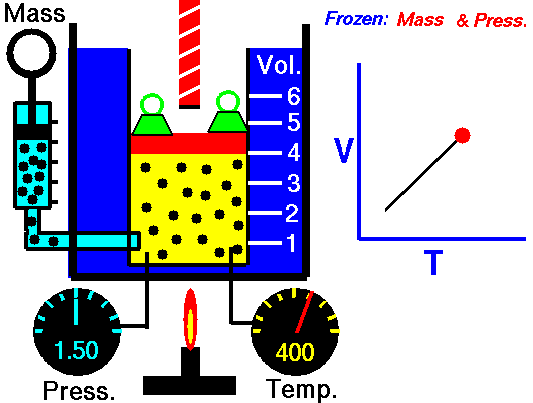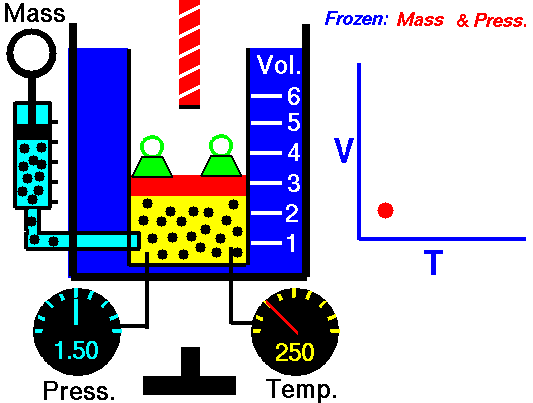
Charles' Law of Volumes

Charles' Law states that the volume of a gas is directly related (directly proportional) to its absolute temperature. In other words, as the temperature goes up, so does the volume. As the temperature decreases, so does the volume. This relationship holds at constant pressure, which means that all measurements of volume and temperature occur at the same pressure.

Charles' Law can be expressed in three ways:

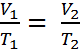Equation #1	Equation #2	Equation #3

V is the volume of the gas
T is the absolute temperature of the gas (measured in kelvin).
k is a constant (which depends on the units of V & T)
Pressure in this relationship is a constant, so is not part of the equation

If the ratio (or fraction) of V and T is always a constant, then we can use an initial pressure and temperature, V₁ and T₁ to solve for volume or temperature at another set of conditions, V₂ or T₂. This is because if V₁/T₁ = k, it must also be true that,

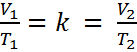
We can remove “k” and we get Equation #2.  A little rearranging give us Equation #3.

It is important to note that you cannot solve this equation with temperatures in °C. You must convert to absolute temperature, or Kelvin (K). This is easy enough to do because, K = °C + 273. Also, volumes can be measured in any units, but whatever they are, both volumes must be in the same units.

Most students find the form of Equation #2 easiest to use. Consider the following word problem:

A gas with a volume of 2.5 Liters and a temperature of 350 Kelvin is cooled to a temperature of 280 Kelvin. What is the new volume?

First we identify the variables, V₁=2.5 L, T₁=350K, T₂ = 280 K and V₂ is unknown. The temperatures absolutely must be in Kelvin. If the temperatures are in °C, simply add 273° to get the temperature in Kelvin. Now, we substitute into Equation #2 and get:

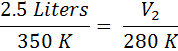
From here, we just cross-multiply the two circled numbers and then divide by the third

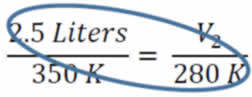
V₂ = (280K x 2.5 L) / 350K = 2.0 L. You can subsitute and cross multiply to solve for any of the four variables.

About Jacques Alexandre César Charles (1746-1823)

Jacques Alexandre César Charles was a French inventor, and mathematician and scientist who worked with gases, among other things. He is credited with many things (some incorrectly), but was correctly given credit for the law stating that the volume of a gas varies directly with the absolute temperature.

It was another scientist who actually formulated this law in 1802, Joseph Gay-Lussac, but Lussac gave Charles the credit, because it came from Charles' unpublished work from the 1780s. In fact, the principles had really first been described almost a century earlier than that by Amontons (1702) and Hauksbee.

Jacques Charles was the first to launch an unmanned baloon filled with hydrogen gas, and in 1783, he and a copilot rode one to an altitued of 1800 feet. The flight lasted over 2 hours and covered about 22 miles. Thousands had watched his takeoff, and he was followed on the ground by horseback. After landing at sunset, he dropped off his copilot and rose again to a height of 10,000 feet, where he was able to see the sun again. He landed again after his rapid ascent caused pain in his ears. He never flew again.