Boyle's Law

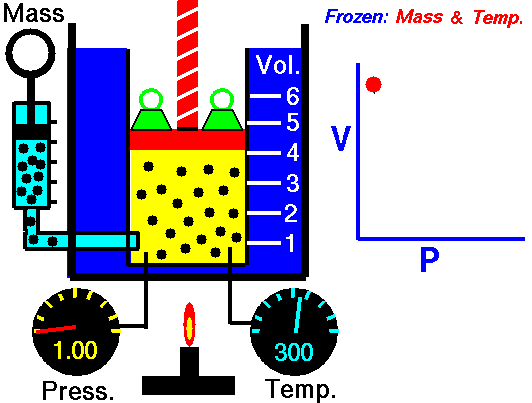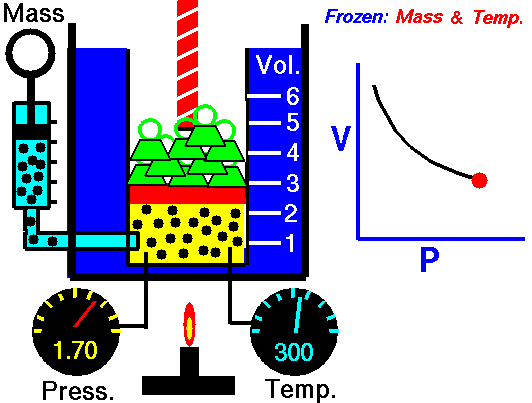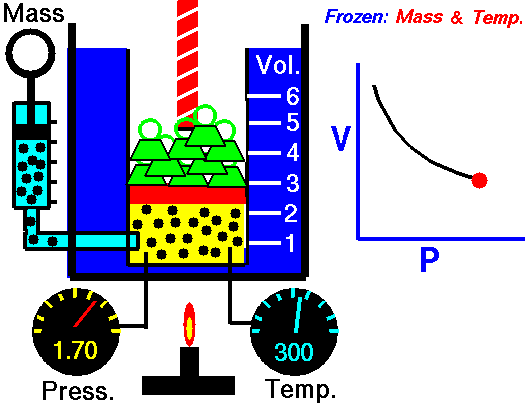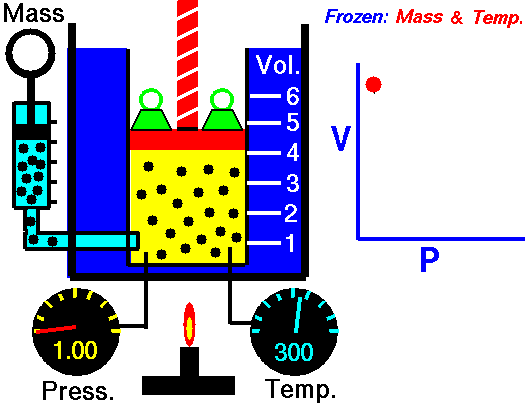
Boyle's Law

Boyle's Law states that the volume of a gas is inversely proportional (inversely related) to it's pressure. In other words, as the pressure goes up, the volume goes down. Pressure squeezes the gas molecules closer together, so the volume becomes smaller. See the animation on the right for a visual idea of how increasing the pressure (the green weights on the lid) affects the volume.

Boyle’s law states that the product of the pressure and volume of a gas is a constant (Equation #1, below).  The value of that constant is unimportant to us, and depends upon the units used to measure the pressure and volume.  However, it is very useful to know that the product is a constant, because that means if pressure goes up, volume must go down. 

Equation #1	Equation #2	Equation #3

We can use Equation #1 and some mathematical magic (the transitive property, Equation #2) to make Equation #3.  Basically, if the product of the pressure and volume at one condition (P₁V₁) equals a constant, then it also equals that same constant at some other condition (P₂V₂).

We can rearrange Equation #3 to solve for any of the four variables.  For instance, if we want to solve for the final pressure (P₂) after changing the volume from V₁ to V₂, the equation becomes,

Equation #4

This equation works with any units for pressure and volume, as long as the units in the first and second conditions are the same.  If the units in 1 & 2 are different, one set will need to be converted.

Consider the example word problem, below:

A piston in the engine of a sports car has a volume of 1.50 liters.  During compression its volume decreases to 0.25 liters.  If the initial pressure is 735 mmHg, what is the final pressure in atmospheres?

First, identify the variables.  I typically require my students to list them down the left side of their worksheets. In this problem, P₁ =735 mmHg, V₁ = 1.50 L, V₂=0.25 L, and P₂ is the unknown.  The problem asks for the answer in atmospheres, so we must decide if we want to convert 735 mmHg to atmospheres first, or convert the answer to atmospheres later.  It really doesn’t matter.  In this example, we will convert later.

We already solved the equation above (#4) for P₂, so all we need to do is substitute values.

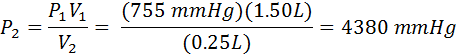
Now we need to convert our final answer to atmospheres.  We need to look at our pressure conversions for that.  We find that 1.00 atm = 760 mmHg, so

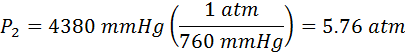
Again, Equation #3 can be solved for any of the 4 variables as it was for P₂ in Equation #4.  If necessary, students can substitute directly into Equation #3 first, and then solve for the unknown variable.

About Robert Boyle

Robert Boyle was an alchemist, though later his works earned him fame in the area of natural philosophy (the precursor to what we now call science). In 1657 he read of another scientist's work with air, and over the next several years performed many experiments of his own. He produced a 'pneumatical engine' and a book was published later describing his work and experiments. It was while defending his work against one critic, Francis Line, that he first makes mention of what was later to become known as 'Boyle's Law' - that the volume of a gas is inversely proportional to it's pressure (though this hypothesis was originally put forth by another scientist, Henry Power, in 1661).

Though he also made great progress in many fields, 'Boyle's Law' is all that many people know of him. He studied hydrostatics and was the first person to describe decompression sickness (now often known as 'the bends'). He studied gems and crystals, electricity, cold, things that glow in the dark, and many other areas of science.

In 1661 he published, 'The Sceptical Chymist: or Chymico-Physical Doubts & Paradoxes', in which he hypothesized that matter was composed of atoms in constant motion and colliding with each other, resulting in all of the phonomena that we observe. He quite nearly describes our modern concept of the atom, when he says:

"I now mean by Elements, as those Chymists that speak plainest do by their Principles, certain Primitive and Simple, or perfectly unmingled bodies; which not being made of any other bodies, or of one another, are the Ingredients of all those call'd perfectly mixt Bodies are immediately compounded, and into which they are ultimately resolved."

He believes that everything we see are compounds of these elements, even what we now know are actual elements, so his understanding is not completely modern; still, his work does a great deal towards modernizing the science of chemistry. For this reason he is considered the father of modern chemistry. Boyle was a devout Christian, and wrote many theological works in addition to his work in natural philosophy. His will left money to support a series of lectures defending the Christian religion.