Avogadro's Law

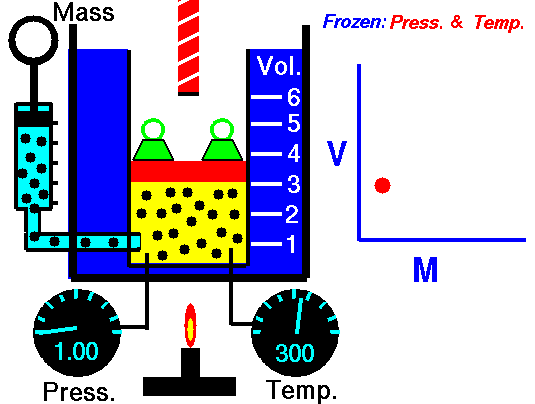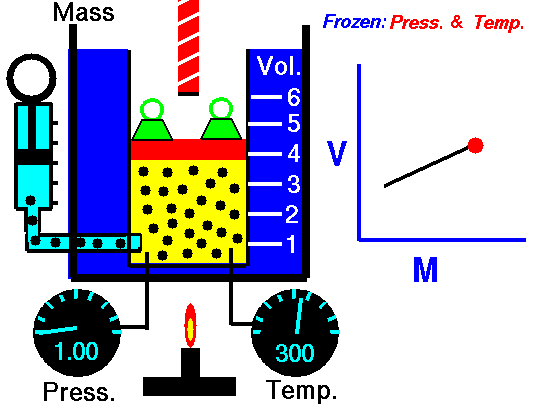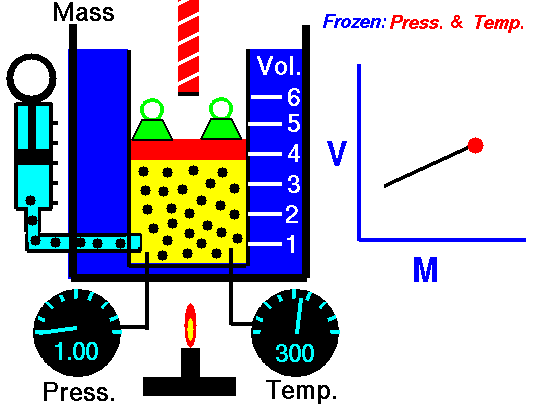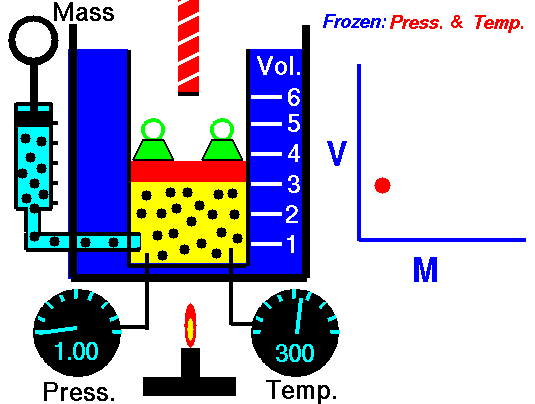
Avogadro's Law

Avogadro's Law (also called Avogadro's hypothesis, or Avogadro's Principle) states that equal volumes of gases at the same temperature and pressure have the same number of molecules of gas. In other words, in an ideal gas, the number of volume of a gas is directly proportional to the number of particles of gas in that volume as long as the temperature and pressure are the same. The molar mass of the gas does not matter. In fact, Avogadro's Principle can be used to determine the molar mass of an unknown gas, since the number of particles can be calculated.

Avogadro's Law can be expressed in three ways:
  

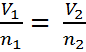Equation #1	Equation #2	Equation #3

The first equation leads to the second and third.   Here is the process. If where,

    V is the volume of the gas,
    n is the number of moles of particles of gas (usually molecules), and
    k is a constant (which depends on the units of P & T)

then, since the ratio (or fraction) of V and n is always a constant, we can use an initial volume and number of moles, V₁ and n₁ to solve for volume or moles at another set of conditions, V₂ or n₂. This is because if V₁/n₁ = k, it must also be true that,

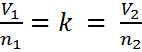
We can remove “k” and we get Equation #2.  A little rearranging can also give us Equation #3; however, most students find the form of Equation #2 easiest to use. Consider the following word problem:

At a constant pressure and temperature a gas which contains 0.350 moles occupies a volume of 11.5 Liters. If another 0.150 moles are added, what will be the new volume?

First we identify the variables, V₁=11.5 L, n₁=0.350 moles, n₂ = (0.350 + 0.150) = 0.500 moles, and V₂ is unknown. The temperature and pressure are unknown, but not important as long as they are constant. Now, we substitute into Equation #2 and get:

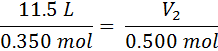
From here, we just cross-multiply the two circled numbers and then divide by the third

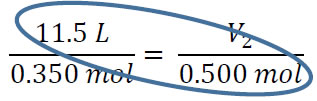
V₂ = (11.5 L x 0.500 mol) / 0.350 = 16.4 L. You can subsitute and cross multiply to solve for any of the four variables as long as temperature and pressure are constant.

About Amedeo Avogadro (1776-1856)

Lorenzo Romano Amedeo Carlo Avogadro di Quaregna e di Cerreto is best known to chemistry students from the number that bears his name, Avogadro's number, 6.022 x 10²³ particles/mole. He did not actually come up with this number, but he did come up with the concept that led to it.

After seeing the results of fellow scientist Joseph Louis Gay-Lussac's published in 1808, Avogadro explanded on his results to derive a hypothesis of his own. Gay-Lussac's Law of Combining Gases said that volumes of gasses involved in reactions could be expressed in simple integers. For example, when 2 volumes of hydrogen and one volume of oxygen make 2 volumes of water. Avogadro expanded this to apply to molecules as well. Avogadro believed that there was a distinction between atoms and molecules and also between molar mass and weight. Combining these ideas, Avogadro believed that a given volume of gas would contain the same number of molecules no matter what their molar mass was. This idea was not generally accepted during Avogadro's lifetime. Another scientist convinced the First International Chemical Congress in 1860.

Avogadro published numerous papers on molecular theory and is hailed as one of the founders of atomic-molecular theory. He never actually determined the value of the number that bears his name. The value of the Avogadro constant was first indicated by Johann Josef Loschmidt in 1865, and the French physicist Jean Perrin determined Avogadro's contant by several different methods in the early 1900's. In 1909 he proposed naming the constant in honor of Avogadro.